Hi, just want to clear up something,
In class we saw an example of proving an isomorphism involving tensor algebras, something of the form . We used the universal property of tensor product, finding a bilinear map which give us map
, then we tried to find an inverse map or just to prove that
was surjective and one to one.
My question is, ¿Aren’t we forgetting to check that satisfies
? I mean, the universal property doesn’t yield an homomorphism of algebras at all. I understand that it’s just a linear map. ..

Servando and Cecilia pointed that fact to me yesterday, so yes, we have to check that.
I disagree that you must check that is a homomorphism.
is a homomorphism. is a homomorphism because the existence of homomorphism
is a homomorphism because the existence of homomorphism  is implied by the bilinearity of the map from the direct product.
is implied by the bilinearity of the map from the direct product. is an isomorphism, then yes you must check that it is bijective.
is an isomorphism, then yes you must check that it is bijective.
I’m open to being corrected, but I understood that the bilinear map “descends” to a homomorphism. If this is correct, then we do not have to validate that
I think that if you want to show that
Ok, on re-reading the lecture notes I have changed my mind. I’ll revise my hw. Thanks for the post!
Moreover, we have to check that is a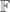 -algebra homomorphism, more than a simple homomorphism, am I right?
-algebra homomorphism, more than a simple homomorphism, am I right?
yimp34, this is a great post, thank you! You are absolutely right.
Moral of the story: Don’t be sloppy! (I was. Sorry. 🙂 I am not very lucid in the morning.)
Let me explain this better:
When you say that something is a “homomorphism”, it is crucial to clarify what kind of homomorphism it is: a vector space homomorphism (which is the same as a linear map), a K-algebra homomorphism, etc. or
or  , it is crucial to know whether you are thinking of these as K-vector spaces, as K-algebras, etc.
, it is crucial to know whether you are thinking of these as K-vector spaces, as K-algebras, etc.
Also, when you write something like
When V,W, and L are K-vectors spaces and you have a bilinear map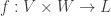 , the universality theorem tells you that it descends to a *linear map*
, the universality theorem tells you that it descends to a *linear map*  of K-vector spaces. We proved this. We used this in examples 1, 2, and 3 to produce linear maps:
of K-vector spaces. We proved this. We used this in examples 1, 2, and 3 to produce linear maps:
We also checked that the first two are in fact isomorphisms *as K-vector spaces*. (In example 2, K=R.)
Now, in examples 1 and 2, I also claimed that these are isomorphisms as K-algebras. To prove that, I should have checked that these are also *K-algebra homomorphisms*. For that I need them to also respect the ring structure, i.e., to satisfy . This is straightforward, but must be checked.
. This is straightforward, but must be checked.
Once we do this, since we already checked that they are bijective, we know they are in fact *isomorphisms* of K-algebras.
In example 3, I only claimed that I had a homomorphism of K-vector spaces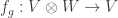 for each linear map
for each linear map 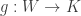 . This is all I needed to prove the next lemma. In fact, if V and W are also K-algebras,
. This is all I needed to prove the next lemma. In fact, if V and W are also K-algebras, 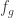 is not necessarily a K-algebra homomorphism. Here is a nice exercise for you:
is not necessarily a K-algebra homomorphism. Here is a nice exercise for you: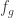 is a homomorphism of K-algebras if and only if g is a homomorphism of K-algebras (i.e. it is also multiplicative).
is a homomorphism of K-algebras if and only if g is a homomorphism of K-algebras (i.e. it is also multiplicative).
Prove that